今回は高1生の初めての壁と言われる（私調べ）、場合分けのある二次関数の最大最小について解説していきたいと思います。この話がわかると、進研模試や河合塾の全統模試で高得点が狙えます。

 

以下では、x₂ の係数 a >0 のときを考えます。a<0 のときは後述します。

 

まずは二次関数の特徴をおさらいします。

 

二次関数のグラフにおける性質

 

①軸について対称。

②頂点が y 軸方向の一番低い位置。（1番小さい値）

③軸から離れれば離れるほど、y 軸方向に上がっていく。

まとめると、最小は頂点で取り、最大は軸からより離れた方で取るわけです。

つまるところ……

 

Theory1

二次関数の最大最小は軸(頂点の x 座標)と定義域の位置関係で決まる。

 

最大と最小で分けて見ていきましょう。

 

Theory2
最小は定義域の中に軸(頂点)が入っているか、左側か右側で場合分け。
Theory3
最大は左右対称となるところより左側か右側で場合分け。

 

具体例を考えます。まずは最小について！

 

(例)関数 y=x₂-4x+4 において、

平方完成をすると、y=(x-2)₂ となるので頂点の座標は (2,0) 、軸の方程式は x=2 ですね。

それに対し、定義域 ① -1≦x≦1 , ② 1/2≦x≦3/2 , ③ 3≦x≦5 を考えていきます。

 

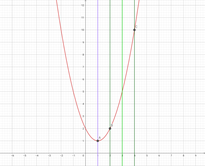
 ① -1≦x≦1 のとき              　  ② 1/2≦x≦3/2 のとき                ③  3≦x≦5 のとき

 

 

 

 

 

 

 

 

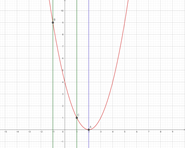
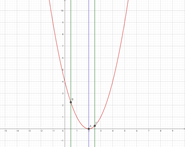
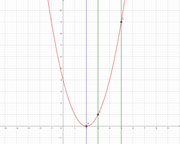
それぞれ、グラフは赤線、軸は紫の線（頂点A）、緑の線が定義域の左端（グラフとの交点B）      と右側（グラフとの交点C）を表しています。

 ①は定義域の右端（点C）で最小、②はグラフの頂点A、③は定義域の左端（点C）で最小となっていることがわかりますね！

 

それに対して、最大は……

(例)関数 y=x₂-4x+4 において

定義域 ① -1≦x≦1 , ② 1≦x≦3 , ③ 3≦x≦5 を考えます。

 

 ① -1≦x≦1 のとき                  ② 1≦x≦3 のとき                     ③ 3≦x≦5 のとき

 

 

 

 

 

 

 

 

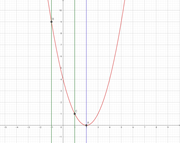
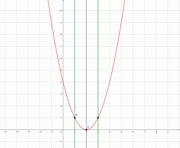
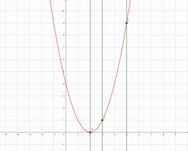
 ①は定義域の左端（点B）で最大、②は軸で左右対称であり定義域の両端（点BとC）で最大、③は定義域の右端（点C）で最大となっていますね！

 

  (x₂ の係数)< 0 のときは、性質が逆（頂点が最大、軸から離れるほど y 軸方向に下がる）なので、Theory 2,3が入れ替わります。

 

Theory4

   ( x₂ の係数)< 0 のとき、

 最大は定義域の中に軸(頂点)が入っているか、左側か右側で場合分け。

 最小は左右対称となるところより左側か右側で場合分け。

 

文字を含む二次関数の最大最小の問題は大きく5つに分けられます。

①頂点の y 座標に文字を含む（例, f(x)=x₂-2x+a , 0≦x≦2）

②定義域の一方に文字、軸は固定（例, f(x)=x₂-2x+2 , 0≦x≦a）

③定義域の両端に1種類の文字、軸は固定（例, f(x)=x₂-2x+2 , a≦x≦a+2）

④定義域は固定、軸に文字を含む（例, f(x)=x₂-2ax+2 , 0≦x≦2）

⑤ x₂ の係数に文字を含む（例, f(x)=ax₂-2x+2 , 0≦x≦2）

 

①はTheory1より、軸と定義域に文字は含まないので最大最小は定まります。

②,③,④はTheory2,3より、場合分けをして最大最小を求めましょう。

⑤はTheory4より、x₂ の係数が正か負か（0か）で場合分けをしましょう。

 

 最後に③の解答例を示して終わります。

 

(問題)(青チャート基本例題80)

aを定数とする。a≦x≦a+2 における関数 f(x)=x₂-2x+2 について最大値を求めよ

 

(考え方)

 定義域の両方に1種類の文字を含んでいるが、

(左端) – (右端) = (a+2)-a=2 より区間の幅が一定で動いている。

区間の中心は左端と右端の中点（平均）で求まるので、Theory2より区間の中心と軸 x=1 より左、一致、右とで場合分け！

 

(解答)

f(x)=x₂-2x+2=(x-1)2+1 よって軸の方程式 x=1 、

 

定義域の中心は、
(a+2)-a2
=a+1     (グラフの明るい緑の線)

 

  (1) a+1<1                           　　　  (2) a+1=1                            　　　 (3) a+1>1

  つまり a<0 のとき                 　　  つまり a=0 のとき                  　　 つまり a>0 のとき

 

 

 

 

 

 

 

 

 

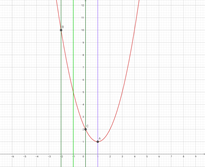
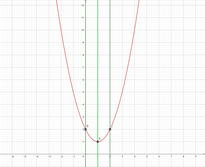
x=a のとき最大                      　　　 x=a,a+2 つまり x=0,2          　　　  x=a+2 のとき最大                                

最大値 f(a)=a₂-2a+2         　　　　   のとき最大で、                           　  最大値

                                              　　     最大値 f(0)=f(2)=2                    　　  f(a+1)=a₂+2a+1

 

 他の問題は教科書やチャートなどの問題集を参考に演習を積み重ねてみてください。

 

 最後に…

慣れない間はグラフも書きながら考えましょう。各問題について、文字を含まないもの（②③なら関数のグラフ、④なら定義域）は先に書いて固定をして、文字を含むもの（②③なら定義域、④なら関数のグラフ）を色々動かして、最大最小の取る位置が変わるところで場合分けをしましょう。

 ただし、Theory1より高さ（ y 方向）とは関係がないので、定義域と x 軸の位置関係だけを考えていきましょう♪

 

(韮崎駅前校 R.T)